Revision 874 as of 2022-04-28 08:43:07
You are not allowed to revert this page!

Clear message

2021/2022-- Letný semester

Prednášajúci

Cvičiace

ROZVRH

Deň

Miestnosť

Od

Do

Link

Učiteľ

Prednáška

pondelok

AB-300

8:00

9:40

viď nižšie

B.Rudolf

Cvičenie

streda

DE-300

10:00

11:40

Konzultačné Cvičenie

utorok

DE-150

10:00

10:50

https://meet.google.com/ycb-tkfr-brh

Čipková, Kossaczká

Konzultačné Cvičenie

utorok

DE-150

11:00

11:50

https://meet.google.com/ikg-xvif-kuc

Čipková, Kossaczká

Konzultačné Cvičenie

utorok

DE-150

12:00

12:50

https://meet.google.com/opk-mpsn-xgd

Čipková, Kossaczká

Rozvrhové akcie typu Miestnosť sú uvedené len pre prípad prechodu na prezenčnú výuku.

Prednáška bude formou videa. Link je uvedený tu:

https://teams.microsoft.com/l/meetup-join/19%3avRRTWeHmlAOV5qKWeI2_Ta2WPE41K-hgZFLi2IBLz-c1%40thread.tacv2/1644491186387?context=%7b%22Tid%22%3a%2225733538-6b16-4aa3-8ed6-297eb79b8e06%22%2c%22Oid%22%3a%225bccfa0f-023f-4387-9848-549f2db466ff%22%7d

Máte možnosť konzultovať s prednášajúcim v stredu od 11.00 do cca 11.40 na linku

https://meet.google.com/jaw-saqo-yai

Nové Oznamy

27.4.2022

Výsledky Testu 5 sú zapísané v priebežnom hodnotení.
Priemerný bodový zisk na 5. teste (vypočítaný zo zúčastnených študentov) je 5,49 bodu.

21.4.2022 Od najbližšej stredy budem na konzultáciách v stredu od 11tej prezentovať príklady zo starších skúšok.

21.4.2022 Informácia o piatom (poslednom) šesťbodovom teste

13.4.2022

Výsledky Testu 4 sú zapísané v priebežnom hodnotení.
Priemerný bodový zisk na 4. teste (vypočítaný zo zúčastnených študentov) je 4,32 bodu.

11.4.2022 Informácia o štvrtom šesťbodovom teste

Prednášky a cvičenia

_12. týždeň_

Prednášky.

Prednáška 10: Prednaska10.pdf
Video Prednáška 11.

Cvičenia.

Príklady 11: Priklady11.pdf

_11. týždeň_

Fubiniho veta na elementárnej oblasti.
Vlastnosti dvojného integrálu.

Prednášky.

Prednáška 9: Prednaska9.pdf
Video Prednáška 10.

(číslovanie sa trošku poposúvalo, ale obsahovo sa video a textová prednáška prekrývajú)

Cvičenia.

Konzultácia Streda: konzultácia11.pdf

_10. týždeň_

Pretože v pondelok je sviatok, prednášky v tomto týždni nie sú.

Konzultačné cvičenia sú normálne podľa rozvrhu. V stredu je prezenčkový test s možnosťou získať bod. Pretože prednášky sú trochu popredu, na cvičeniach sa riešia príklady z 9. týždňa.

_9. týždeň_

Dvojný integrál, pokračovanie. Fubiniho veta na obdĺžniku.

Prednášky.

Video Prednáška 9.
Textová prednáška, ktorá je obsahom videa je v minulom týždni.
Aj obsah cvičení je o týždeň popredu, resp. video prednášky mierne zaostávajú.

Cvičenia.

Cvičenie9riešené.
Neriešené Príklady 9: Priklady9.pdf

_8. týždeň_

Absolútne extrémy funkcie viacerých premenných.
Dvojný integrál. Úvodné pojmy. Miera oblasti v rovine.

Prednášky.

Prednáška 8: Prednaska8.pdf
Video Prednáška 8.

Cvičenia.

Cvičenie8riešené.
Neriešené Príklady 8: Priklady8.pdf

_7. týždeň_

Viazané extrémy funkcie viacerých premenných.

Prednášky.

Prednáška 7: Prednaska7.pdf
Video Prednáška 7.

Cvičenia.

Cvičenie7riešené.
Neriešené Príklady 7: Priklady7.pdf

_6. týždeň_

Lokálne extrémy funkcie viacerých premenných.
Stacionárne body.
Kritériá pre určenie lokálneho extrému pomocou druhého diferenciálu a Taylorovho polynómu druhého stupňa.

Prednášky.

Prednáška 6: Prednaska6.pdf
Video Prednáška 6.
Vo videoprednáške 6 je v čase 1.15 nesprávne znamienko, zmiešaná derivácia má mať koeficient +2c. Pre ďalšie odvodenie je tento preklep nepodstatný, ďalej sa zmení znamienko vnútri zátvorky kvadratického výrazu.

Cvičenia.

Cvičenie6riešené.
Neriešené Príklady 6: Priklady6.pdf

_5. týždeň_

Hovoríme o derivovaní zloženej funkcie viacerých premenných.
Reťazové pravidlo demonštrujeme na niektorých príkladoch.
Definujeme druhý diferenciál a Taylorov polynóm druhého stupňa.
Ide o pojmy, ktoré použijeme v kapitole o lokálnych extrémoch.

Prednášky.

Prednáška 5: Prednaska5.pdf
Video Prednáška 5.
Vo videoprednáške 5 je v čase 32:30 preklep v označení parciálnej derivácie 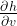\ \large${\partial h}\over{\partial v}$.

Cvičenia.

Cvičenie5riešené.
Neriešené Príklady 5: Priklady5.pdf

_4. týždeň_

V tomto týždni dokončujeme kapitolu diferencovateľnosť funkcie a 1. diferenciál tým, že predvedieme ešte dva príklady.
A pokračujeme kapitolou derivácia v smere a gradient.
Videoprednášku som natiahol viac ako sa patrí. Preto je aj taká posekaná.
Aj tak sa mi tam nevošiel príklad na gradient, ako smer maximálneho rastu.
Nájdete ho v textovej prednáške 4 na konci textu.

Prednášky.

Prednáška 4: Prednaska4.pdf
Video Prednáška 4.
Chyba vo videu:
V prednáške 4 v čase 58:10 pri definícii gradientu je v poslednom riadku na tabuli chyba. Namiesto 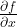\large${\partial f}\over{\partial x}$ má byť druhá zložka gradientu \large${\partial f}\over{\partial y}$.

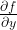Cvičenia.

Cvičenie4riešené.
Neriešené Príklady 4: Priklady4.pdf

_3. týždeň_

V treťom týždni začíname kapitolu diferenciálny počet funkcie viac premenných.
Zavedieme pojem parciálna derivácia.
Naučíme sa hľadať dotykovú rovinu ku grafu funkcie 2 premenných.
Dotykovú rovinu majú len diferencovateľné funkcie, povieme čo je diferencovateľnosť funkcie. Zavedieme tiež 1. diferenciál.

Prednášky.

Prednáška 3: Prednaska3.pdf
Video Prednáška 3.

Cvičenia.

Cvičenie3riešené.
Neriešené Príklady 3: Priklady3.pdf

_2. týždeň_

Témou prednášky je limita a spojitosť funkcie viacerých premenných.
(Rovnaká podstata, ako pri funkcii jednej premennej, ale aj významné rozdiely.)

Prednášky.

Prednáška 2: Prednaska2.pdf
Video Prednáška 2.

Cvičenia.

Cvičenie2riešené.
Neriešené Príklady 2: Priklady2.pdf

_1. týždeň_

Pojem funkcia viacerých premenných a základné pojmy s ňou súvisiace.
Geometrickú predstavu o jej grafe v prípade dvoch premenných x,y budujeme pomocou pojmov vrstevnice, parciálne funkcie, rezy.

Prednášky.

Prednáška 1: Prednaska1.pdf
Video Prednáška 1.

Cvičenia.

Cvičenie1riešené.
Neriešené Príklady 1: Priklady1.pdf

Skúste výpočty a prípadne kreslenie grafov použitím https://www.wolframalpha.com/examples/Math.html
Najmä pre priestorovú predstavu funkcie dvoch premenných je vykreslenie grafov užitočné.

Oznamy

4.4.2022
V stredu je prezenčkový test s možnosťou bonusového bodu.

30.3.2022

Výsledky Testu 3 sú zapísané v priebežnom hodnotení. Priemerný bodový zisk (vypočítaný zo zúčastnených študentov) je 5.6 bodu.

30.3.2022 Ak ste absolvovali druhý, test tak sa Vás náhradný termín testu netýka. (Aj keď ste pravdepodobne dostali o ňom správu.)

25.3.2022 Informácia o treťom šesťbodovom teste

17.3.2022
Výsledky Testu 2 sú zapísané v priebežnom hodnotení. Priemerný bodový zisk (vypočítaný zo zúčastnených študentov) je 5.0 bodu.

11.3.2022 Informácia o druhom šesťbodovom teste

2.3.2022
Výsledky Testu 1 sú zapísané v priebežnom hodnotení. Priemerný bodový zisk (vypočítaný zo zúčastnených študentov) je 5.2 bodu.

24.2.2022

Na budúci týždeň v stredu 2.marca 2022 bude (v čase cvičenia z M2), o 10.00 prvý 6 bodový test z Matematiky 2.

Cesta: E-learning -> Testy a skúšanie -> nazov testu
Obsah: funkcia viacerých premenných - učivo od začiatku semestra po limity (vrátane)
Forma: test s otázkami s výberom správnej odpovede/správnych odpovedí, doplnenie správnej odpovede
Trvanie: cca 30-40 minút (upresníme)
Hodnotenie: max 6 bodov

Milí študenti,

Podľa súčasných informácií aj v tomto semestri pobeží výuka dištančným spôsobom.
Tu je niekoľko (veľa) informácií o priebehu semestra v predmete Matematika 2 pre informatikov (M2I).
Hodinový rozsah predmetu je 2 hodiny prednášok + 2 hodiny cvičení týždenne, celkovo 12 týždňov.

Prednáška.

Prednáška je každý týždeň v Pondelok od 8.00 do 9.40, 1h 40min čistého času. Bude vo forme videa a budem ju vysielať v čase podľa rozvrhu hodín.
Vysielanie bude cez MS Teams. Okrem toho budú videá prednášok prístupné spolu s ostatnými študijnými materiálmi na stránke predmetu M2I:

http://matika.elf.stuba.sk/KMAT/Matematika2/ParalelkaA

Tu si ich môžete stiahnuť a pozrieť v ľubovoľnom čase a pravdepodobne v trochu lepšej kvalite. Odporúčam pravidelné sledovanie a neodkladanie na „neskôr“.

Na stránke predmetu budú aj prednáškové texty.
Ak budete potrebovať, môžete obsah prednášok konzultovať so mnou v čase, ktorý naplánujem podľa podoby rozvrhu. Táto aktivita je dobrovoľná.

Cvičenia.

Cvičenia majú v rozvrhu jednu dvojhodinovku týždenne v Stredu 10.00-11.40. V tomto čase bude Vašou úlohou pozrieť si videá, ktoré obsahujú riešenie niektorých príkladov, naštudovať riešené príklady a skúsiť riešiť neriešené. Jedny aj druhé budú tiež na stránke predmetu.
Počas spoločnej dvojhodinovky budú v nepárnych týždňoch semestra, počnúc tretím týždňom, aj krátke bodované testy každý za 6 bodov, celkovo za 30 bodov.
Tieto testy sú súčasťou Priebežného hodnotenia a je na nich potrebné získať (samozrejme čo najviac, lebo sa body rátajú aj do skúšky) aspoň 15 bodov, aby ste sa mohli po skončení semestra zúčastniť na záverečnej skúške.
V párnych týždňoch dostanete v tomto čase krátku úlohu, ktorá bude slúžiť ako prezencia. Pri dobrom riešení môžete získať bonusový bod.
V druhej časti tejto dvojhodinovky bude možnosť online konzultovať s prednášajúcim na linku

https://meet.google.com/jaw-saqo-yai

prípadné nejasnosti.

Konzultačné cvičenia.

V utorok o 10.00, 11,00 a 12.00 sú v rozvrhu tri termíny pre 1hodinovú konzultáciu s cvičiacimi učiteľmi, kde si budete môcť overiť svoje riešenia, klásť otázky k príkladom, prípadne požiadať o ukážku riešenia niektorých príkladov, ktoré Vám nešli riešiť.
Na túto 1hodinu budete rozdelení do menších skupín. Rozdelenie Vám zverejníme na začiatku prvého týždňa semestra.
Linky na tieto cvičenia sú na MOODLE

https://elearn.elf.stuba.sk/moodle/course/view.php?id=674 .

Odkazy na jednohodinové konzultácie budú zverejnené aj na stránke predmetu

http://matika.elf.stuba.sk/KMAT/Matematika2/ParalelkaA

kde je umiestnený kurz Matematika 2 - paralelka AI, ktorý budeme používať na offline komunikáciu.
Prihlásenie do MOODLE prebieha rovnako ako do AIS (rovnaké prihlasovacie meno a rovnaké heslo, ako máte tam) a na prihlásenie do kurzu použite (bude to potrebné iba pri prvom vstupe) heslo M2Rudolf. Čo tam nájdete:

Skúška.

Záverečné skúška bude prezenčná, pokiaľ to bude možné.
Základné informácie o skúške sú na stránke predmetu, podrobné informácie o nej dostanete pred skončením semestra.

Prajeme Vám potešenie z možnosti študovať matematiku.

Literatúra

1. SATKO, L. -- ŠULKA, R. Matematická analýza 2 : Diferenciálny a integrálny počet funkcie viac premenných. Bratislava: STU v Bratislave, 1995. 160 s.
2. MORAVSKÝ, L. -- MORAVČÍK, J. -- ŠULKA, R. Matematická analýza 2. Bratislava: Alfa, 1992. 552 s.
3. BRABEC, J. -- HRŮZA, B. Matematická analýza II. Praha: SNTL, 1986. 579 s.
4. MARKO, Ľ. Matematická analýza online. [online]. 2003. URL: http://www.fei.stuba.sk/~marko.

1. Edwards, C.H., Penney, D.E.: Calculus and Analytic Geometry, (3rd edition), Prentice Hall International, New York 1990
2. Glyn, J.: Modern engineering mathematics, Addison Wesley, 2008

Ďalšie príklady môžete nájsť v elektronickej literature uvedenej nižšie.
Tiež v zbierke Eliáš, Horvath, Kajan: Zbierka úloh z vyššej matematiky 3. resp. 4. diel. (dostupná napr. v študovni)

Ďalšia literatúra

Tu je elektronická verzia literatúry, (autor Doc. RNDr. Ladislav Satko CSc.):
(pre tento predmet sú relevantné kapitoly 3 a 4. Kvôli pohodliu čitateľa sú predchádzajúce kapitoly 1 a 2 z textu vypustené)
Matematická analýza - pdf

Podmienky účasti na skúške z M2

Skúšky

Fórum