2024/2025 -- Letný semester
Prednášajúci
- doc. RNDr. Boris Rudolf, CSc., boris.rudolf[at]stuba.sk, miestnosť A - 403
Cvičiaci
RNDr. Karla Čipková, PhD., karla.cipkova[at]stuba.sk, miestnosť A - 424
- RNDr. Michal Zákopčan, PhD., michal.zakopcan[at]stuba.sk, miestnosť A - 401
Oznamy
30.5.2025
Výsledky opravného termínu skúšky sú zapísané v AIS.
nahliadnutie do písomiek bude v utorok 1.7 od 13.00 v miestnosti AB-300.
Ak bude štátnicová komisia trvať dlhšie, ako do 13.00, bude treba na nahliadnutie počkať.
4.6.2025
Opravný termín skúšky bude v
piatok 27. júna 2025 od 11.00 v miestnosti AB-300.
Priebeh skúšky a pokyny sú rovnaké, ako na riadnom termíne. (Pozri oznam z 2. mája.)
Študenti, ktorí na riadnom termíne neuspeli, sa na opravný termín nikde neprihlasujú, s ich účasťou počítame automaticky.
29.5.2025
Známky z riadneho termínu skúšky sú zapísané v AIS.
Získané body na písomke nájdete v priebežnom hodnotení.
Nahliadnutie do opravených písomiek bude v pondelok 2.6. o 16:00 v miestnosti AB-150.
15.5.2025
Rozpis pre účasť na skúške do jednotlivých miestností je tu: RozpisRT2025.pdf.
2.5.2025
Podľa súčasného návrhu bude riadny termín skúšky v
pondelok 26. mája 2025 o 14:00 v miestnostiach AB-300, BC-300 a CD-300
Na skúške bude 4-5 príkladov celkovo za 70 bodov.
Príklady môžu mať časti a, b,... Témy sú nasledovné:
- limita a spojitosť
- diferenciálny počet
- lokálne, viazané a absolútne extrémy
- dvojný integrál na elementárnej množine M (typu xy alebo yx)
- dvojný integrál pomocou substitúcie do polárnych súradníc
Na skúšku si prineste cca 10 papierov formátu A4, na každý napíšte Vaše meno a priezvisko.
Nie sú povolené žiadne iné pomôcky.
Riešenie prvých dvoch príkladov bude treba odovzdať cca po 1 hodine v polovici skúšky.
Celkový odhad trvania skúšky je cca 2 hodiny.
Hodnotenie zo skúšky vložíme do AIS po opravení a obodovaní všetkých príkladov.
Bodové hodnotenie študenta je súčtom bodov zo semestra a bodov zo záverečnej skúšky. Známka je odvodená od počtu získaných bodov.
2.5.2025
Výsledky 2. testu sú zapísané v AIS. Nahliadnuť do opravených písomiek budete môcť na cvičení vo štvrtok.
Priemerný bodový výsledok testu je 10,11 bodu.
29.4.2025
Náhradný a opravný 1. aj 2. test z Matematiky 2 bude v pondelok 12.5.2025 v čase od 12.00 do 12.50 v miestnosti AB-300.
Na test sa treba prihlásiť u prednášajúceho. Obsah bude podobný, ako na riadnych testoch.
11.4.2025
Druhý priebežný test z Matematiky 2 bude v pondelok 28.4.2025 v čase od 12.00 do 12.50.
Budú na ňom 3 úlohy spolu za 15 bodov.
Bude mať príklady z oblastí: Lokálne, viazané, absolútne extrémy, Elementárne oblasti, Dvojný integrál na obdĺžniku.
Rozdelenie do miestností AB-300, CD-300, DE-300 a obsah testu nájdete tu:
rozpis2test.pdf
starší test - ukážka: test2.pdf
27.3.2025
Výsledky 1. testu sú zapísané v AIS. Nahliadnuť do opravených písomiek budete môcť na cvičení vo štvrtok.
Priemerný bodový výsledok testu je 11,78 bodu.
Druhý test plánujeme na pondelok 28.4.2025 v čase od 12.00 do 12.50.
4.3.2025
Prvý priebežný test z Matematiky 2 bude v pondelok 24.3.2025 v čase od 12.00 do 12.50.
Budú na ňom 3 úlohy spolu za 15 bodov.
Bude mať príklady z oblastí: Limita a spojitosť, dotyková rovina a diferencovateľnosť a derivácia v smere a gradient.
Rozdelenie do miestností a obsah testu nájdete tu:
rozpis1test.pdf
starší test - ukážka: test.pdf
Prednášky a cvičenia
Tu nájdete zadanie a riešenie staršej skúšky z minulosti. Obsahovo sa zadanie nebude veľmi líšiť, budú 4 alebo bude 5 príkladov.
12. týždeň
Niektoré aplikácie dvojného integrálu.
Prednášky.
Prednáška 11: Prednaska11.pdf
Video Prednáška 12.
Cvičenia.
Neriešené Príklady 11: Priklady11.pdf
Vo videu je preklep v čase cca 1:12-1:13. Horná hranica integrálu je napísaná ako  namiesto správneho
namiesto správneho 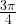 . Ďakujem za upozornenia.
. Ďakujem za upozornenia.
11. týždeň
V poslednom aprílovom týždni nie je prednáška.
Tieto témy budú na prednáške až 7.mája.
Bolo by dobre, keby ste si pred cvičením, ktoré bude 30. apríla,
pozreli obsah prednášky o substitúcii do polárnych súradníc.
Substitúcia v dvojnom integráli.
Substitúcia použitím polárnych súradníc.
Prednášky.
Prednáška 11: Prednaska10.pdf
Video Prednáška 11.
Cvičenia.
Cvičenie11riešené.
Neriešené Príklady 10: Priklady10.pdf
10. týždeň
Fubiniho veta na elementárnej oblasti.
Vlastnosti dvojného integrálu.
Prednášky.
Prednáška 10: Prednaska9.pdf
Video Prednáška 10.
(číslovanie sa trošku poposúvalo, ale obsahovo sa video a textová prednáška prekrývajú)
Cvičenia.
9. týždeň
Dvojný integrál, pokračovanie. Fubiniho veta na obdĺžniku.
Prednášky.
Video Prednáška 9.
Textová prednáška, ktorá pokrýva obsah videa je v minulom týždni prednáška č 8.
Aj obsah cvičení je o týždeň popredu, resp. video prednášky a aj živé prednášky mierne zaostávajú oproti textom.
Cvičenia.
Cvičenie9riešené.
Neriešené Príklady 9: Priklady9.pdf
8. týždeň
Absolútne extrémy funkcie viacerých premenných.
Dvojný integrál. Úvodné pojmy. Miera oblasti v rovine.
Prednášky.
Prednáška 8: Prednaska8.pdf
Video Prednáška 8.
Cvičenia.
Cvičenie8riešené.
Neriešené Príklady 8: Priklady8.pdf
7. týždeň
Viazané extrémy funkcie viacerých premenných.
Prednášky.
Prednáška 7: Prednaska7.pdf
Video Prednáška 7.
Cvičenia.
Cvičenie7riešené.
Neriešené Príklady 7: Priklady7.pdf
6. týždeň
Lokálne extrémy funkcie viacerých premenných.
Stacionárne body.
Kritériá pre určenie lokálneho extrému pomocou druhého diferenciálu a Taylorovho polynómu druhého stupňa.
Prednášky.
Prednáška 6: Prednaska6.pdf
Video Prednáška 6.
Vo videoprednáške 6 je v čase 1.15 nesprávne znamienko, zmiešaná derivácia má mať koeficient +2c. Pre ďalšie odvodenie je tento preklep nepodstatný, ďalej sa zmení znamienko vnútri zátvorky kvadratického výrazu.
Cvičenia.
Cvičenie6riešené.
Neriešené Príklady 6: Priklady6.pdf
5. týždeň
Hovoríme o derivovaní zloženej funkcie viacerých premenných.
Reťazové pravidlo demonštrujeme na niektorých príkladoch.
Definujeme druhý diferenciál a Taylorov polynóm druhého stupňa.
Ide o pojmy, ktoré použijeme v kapitole o lokálnych extrémoch.
Prednášky.
Prednáška 5: Prednaska5.pdf
Video Prednáška 5.
Vo videoprednáške 5 je v čase 32:30 preklep v označení parciálnej derivácie 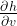 .
.
Cvičenia.
Cvičenie5riešené.
Neriešené Príklady 5: Priklady5.pdf
4. týždeň
V tomto týždni dokončujeme kapitolu diferencovateľnosť funkcie a 1. diferenciál tým, že predvedieme ešte dva príklady.
A pokračujeme kapitolou derivácia v smere a gradient.
Videoprednášku som natiahol viac ako sa patrí. Preto je aj taká posekaná.
Aj tak sa mi tam nevošiel príklad na gradient, ako smer maximálneho rastu.
Nájdete ho v textovej prednáške 4 na konci textu.
Prednášky.
Prednáška 4: Prednaska4.pdf
Video Prednáška 4.
Chyba vo videu:
V prednáške 4 v čase 58:10 pri definícii gradientu je v poslednom riadku na tabuli chyba. Namiesto 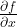 má byť druhá zložka gradientu
má byť druhá zložka gradientu 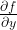 .
.
Cvičenia.
Cvičenie4riešené.
Neriešené Príklady 4: Priklady4.pdf
3. týždeň
V treťom týždni začíname kapitolu diferenciálny počet funkcie viac premenných.
Zavedieme pojem parciálna derivácia.
Naučíme sa hľadať dotykovú rovinu ku grafu funkcie 2 premenných.
Dotykovú rovinu majú len diferencovateľné funkcie, povieme čo je diferencovateľnosť funkcie.
Zavedieme tiež 1. diferenciál funkcie viac premenných.
Prednášky.
Prednáška 3: Prednaska3.pdf
Video Prednáška 3.
Cvičenia.
Cvičenie3riešené.
Neriešené Príklady 3: Priklady3.pdf
2. týždeň
Témou prednášky je limita a spojitosť funkcie viacerých premenných.
(Podstata pojmov je rovnaká ako pri funkcii jednej premennej, ale všimneme si aj významné rozdiely najmä pri limite zúženia na krivku.)
Prednášky.
Prednáška 2: Prednaska2.pdf
Video Prednáška 2.
Cvičenia.
Cvičenie2riešené.
Neriešené Príklady 2: Priklady2.pdf
1. týždeň
Pojem funkcia viacerých premenných a základné pojmy s ňou súvisiace.
Geometrická predstava o grafe funkcie dvoch premenných x,y. Pojmy vrstevnica, parciálna funkcia.
Prednášky.
Prednáška 1: Prednaska1.pdf
Video Prednáška 1.
Cvičenia.
Cvičenie1riešené.
Neriešené Príklady 1: Priklady1.pdf
Skúste výpočty a prípadne kreslenie grafov použitím https://www.wolframalpha.com/examples/Math.html
Najmä pre priestorovú predstavu funkcie dvoch premenných je vykreslenie grafov užitočné.
Skriptum
Tu nájdete spísané prednášky do podoby skrípt.
Matematika 2
Literatúra
- Základná:
1. SATKO, L. -- ŠULKA, R. Matematická analýza 2 : Diferenciálny a integrálny počet funkcie viac premenných. Bratislava: STU v Bratislave, 1995. 160 s.
2. MORAVSKÝ, L. -- MORAVČÍK, J. -- ŠULKA, R. Matematická analýza 2. Bratislava: Alfa, 1992. 552 s.
3. BRABEC, J. -- HRŮZA, B. Matematická analýza II. Praha: SNTL, 1986. 579 s.
4. MARKO, Ľ. Matematická analýza online. [online]. 2003. URL: http://www.fei.stuba.sk/~marko.
- Odporúčaná:
1. Edwards, C.H., Penney, D.E.: Calculus and Analytic Geometry, (3rd edition), Prentice Hall International, New York 1990
2. Glyn, J.: Modern engineering mathematics, Addison Wesley, 2008
Ďalšie príklady môžete nájsť v elektronickej literature uvedenej nižšie.
Tiež v zbierke Eliáš, Horvath, Kajan: Zbierka úloh z vyššej matematiky 3. resp. 4. diel. (dostupná napr. v študovni)
Ďalšia literatúra
Tu je elektronická verzia literatúry, (autor Doc. RNDr. Ladislav Satko CSc.):
(pre tento predmet sú relevantné kapitoly 3 a 4. Kvôli pohodliu čitateľa sú predchádzajúce kapitoly 1 a 2 z textu vypustené)
Matematická analýza - pdf
Staré oznamy
Skúška a Podmienky účasti na skúške z M2
Celkový počet bodov na skúške z M2 je 100.
Počas semestra budú 2 testy, na ktorých môže študent získať 30 bodov a prípadne bonusové body naviac.
Orientačný termín: 1.test v šiestom týždni semestra, 2.test v desiatom týždni semestra.Nutnou podmienkou účasti na skúške z M2 je počas semestra získať aspoň 15 bodov.
Skúška je písomná. Pozostáva z úloh na riešenie.
Na záverečnej písomke môžete získať 70 bodov.
Podvádzanie pri skúške má za následok hodnotenie nevyhovel.
- Rozsah príkladov a ich bodové hodnotenie upresníme pred koncom semestra.
Neúčasť na skúške je potrebné ospravedlniť na PGO najneskôr do piatich dní a doložiť patričným dokladom. Pokiaľ sa študent neospravedlní do daného termínu, nemá nárok na náhradný termín.
Na písomkách a na skúške sa nepoužívajú žiadne pomôcky.
 Oddelenie matematiky
Oddelenie matematiky