Riešenia prémií z predmetu Algebry a grafy

Prémia 1

(6 bodov) Dokážte, že ak A,B,C sú množiny také, že

Math(A\cup B=B\cup C=A\cup C)

a zároveň

Math(A\cap B=B\cap C=A\cap C,) potom platí A=B=C.

Riešenie (Smolinský)

Prémia 2

(6 bodov) Nájdite systém (množinu množín) Math(\{A_i\}_{i\in I}) (I je množina indexov) s takýmito vlastnosťami:

1. Pre každú konečnú množinu Math(F\subseteq I) platí, že Math(\big\cap_{i\in F}A_i\not =\emptyset).

2. Math(\big\cap_{i\in I}A_i=\emptyset).

Komentár: Bolo dosť rozšírené presvedčenie, že I je konečná množina. Pre konečné I však riešenie neexistuje! Ak položíme F=I, dostaneme totiž toto:

1. Math(\big\cap_{i\in I}A_i\not =\emptyset).

2. Math(\big\cap_{i\in I}A_i=\emptyset).

To je pochopiteľne v spore. Teda I musí byť nekonečná.

Riešenie (Andruška)

Prémia 3

(10 bodov) Dokážte De Morganov zákon

Math((A\cup B)^c=A^c\cap B^c)

pre množiny čisto pomocou základných rovností uvedených na prednáške. Okrem základných rovností môžete použit idempotentnosť prieniku, resp. zjednotenia:

{$ A\cap A=A,~A\cup A=A $}

Riešenia s mojimi komentármi

Prémia 4

(8 bodov) Zistite, či je relácia {$\rho\subseteq R^{+\times R}+$}, kde {$R^+$} je reálny interval {$(0,\infty)$} daná predpisom

{$x\rho y:\Leftrightarrow \sqrt[x]{y}\leq\sqrt[y]{x}$}

reflexívna, symetrická, antisymetrická, tranzitívna.

Riešenia s mojimi komentármi

Prémia 5

(5 bodov)

Nájdite poset, ktorý má práve jeden maximálny prvok a nemá žiaden minimálny.

Riešenie: (Poláčik)

Prémia 6

(8 bodov)

Na množine všetkých kružníc v rovine je definovaná operácia {$*$} daná predpisom

takto: {$k_1 *k_2$}:=kružnica s najmenším možným polomerom, obsahujúca {$k_1,k_2$} vo svojom vnútri.

Zistite, či {$*$} je asociatívna.

Riešenie (Nemsila) nemsila_6.pdf

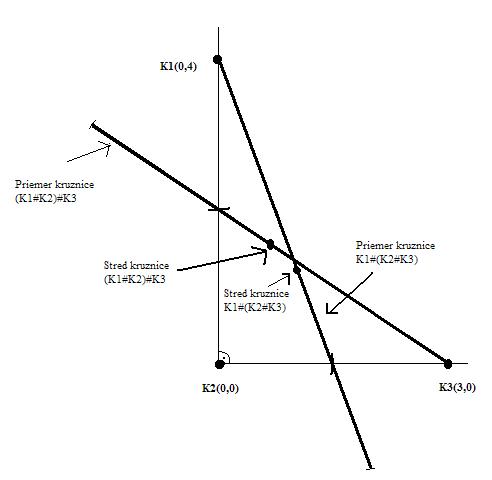
Riešenie (Adam Pavlík). K1,K2,K3 majú nulový polomer.

Prémia 7

(12 bodov)

Dokážte, že ak H je podgrupa (Z,+), potom H=k.Z pre nejaké prirodzené k.

Riešenie Pali Spacek (?) + iné riešenie