Lineárna algebra 2
2025/2026 zimný semester
pre študijný program Aplikovaná informatika
Kód predmetu v MS Teams: dcp91cv
Informačný list
Garant predmetu
Vyučujúci
doc. Mgr. Ján Karabáš, PhD., prednášky (1-6)
- doc. RNDr. Jana Šiagiová, PhD., prednášky (7-12)
Mgr. Katarína Hriňáková, PhD., cvičenia
V prípade akýchkoľvek problémov, otázok a nejasností sa obracajte predovšetkým na prednášajúcich!
Rozvrh
Deň |
Od |
Do |
Miestnosť |
Krúžok |
Vyučujúci |
pondelok |
17:00 |
19:00 |
ab300 |
API |
Karabáš/Šiagiová |
utorok |
13:00 |
15:00 |
e702 |
3bc_API |
Katarína Hriňáková |
utorok |
15:00 |
17:00 |
e702 |
2bc_API |
Katarína Hriňáková |
Konzultácie
Konzultácie k prednáškam:
- podľa individuálnej dohody s prednášajúcim,
- J. Karabáš: A411, pondelok 14:00-16:00, utorok 9:00-11:00
- MS Teams
Konzultácie k cvičeniam:
- podľa individuálnej dohody s cvičiacim
- MS Teams
Prehľad tém
Celé čísla (Aluffi, kapitola 1; Rotman, sekcie 1.1,1.3,1.4; Gallian kapitola 1)
prirodzené čísla; celé čísla; dobré usporiadanie; deliteľnosť; induktívne myslenie; princíp najmenšieho svedka; matematická indukcia; celočíselné delenie; najväčší spoločný deliteľ celých čísel; súdeliteľnosť; prvočísla; rozklad čísla na nerozložiteľné činitele; hľadanie prvočísel; Bézoutova rovnosť; rozšírený Euklidov algoritmus; základná veta aritmetiky; najmenší spoločný násobok celých čísel.Kongruencie (Aluffi, kapitola 2; Rotman, sekcie 1.5, 1.2)
kongruencie; rozklad množiny celých čísel modulo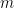 ; binárne operácie modulo
; binárne operácie modulo 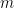 ; aplikácia - ISBN; lineárne kongruencie; riešenie kongruencií; aplikácia - samoopravný kód; čínska zvyšková veta; invertibilné čísla modulo
; aplikácia - ISBN; lineárne kongruencie; riešenie kongruencií; aplikácia - samoopravný kód; čínska zvyšková veta; invertibilné čísla modulo 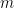 , Eulerova
, Eulerova 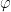 -funkcia; malá Fermatova veta; Fermatov test na zložené čísla; modulárne umocňovanie; problém diskrétneho logaritmu; aplikácia - Diffie-Hellmannova schéma.
-funkcia; malá Fermatova veta; Fermatov test na zložené čísla; modulárne umocňovanie; problém diskrétneho logaritmu; aplikácia - Diffie-Hellmannova schéma. Okruhy a polia (Aluffi, kapitoly 3 a 4)
okruh; jednoznačnosť neutrálnych prvkov; negatívny prvok; všeobecný asociatívny zákon; aditívny rád prvku, charakteristika okruhu; komutatívne okruhy; delitele nuly; obor integrity; invertibilné a inverzné prvky, mocnina prvku; pole; pramy súčin okruhov; podokruh; homomorfizmus okruhov, izomorfizmus.
Pozor! Definícia okruhu sa v tejto prednáške mierne odlišuje od definície, ktorá je uvádzaná v literatúre. Podľa niektorých kníh (napr. Katriňák) je náš okruh zavedený ako 'okruh s jednotkou'. Tento rozdel spôsobuje malé rozdiely v argumentácii. Napríklad, nevýhodou nšej definície je, že musíme ošetriť špeciálne triviálny okruh a napríklad množina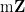 u nás okruhom nie je. Výhodou je, že dôkazy tvrdení sú u nás kratšie, keďže máme 'silnejšiu aritmetiku'.
u nás okruhom nie je. Výhodou je, že dôkazy tvrdení sú u nás kratšie, keďže máme 'silnejšiu aritmetiku'. Faktorové okruhy (Aluffi, sekcie 5.1-5.5)
dekompozícia zobrazenia, kanonická dekompozícia; jadro homomorfizmu; ideál v okruhu, generátory ideálu, hlavný ideál; kongruencia podľa ideálu, kvocient okruhu, faktorový okruh; kanonická dekompozícia homomorfizmu; prvá veta o izomorfizme. okruhov, komplexné čísla (definícia)Ideály a okruhy, okruhy s delením (Aluffi, sekcie 5.6,5.7, kapitola 6)
Operácie s ideálmi v okruhu; druhá veta o homomorfizme okruhov, čínska zvyšková veta; tretia veta o homomorfizme; primitívny ideál v okruhu, maximálny ideál v okruhu; deliteľnost v okruhu, najväčší spoločný deliteľ; primitívne a ireducibilné prvky v okruhu; Euklidovské okruhy; okruhy hlavných ideálov (PID); Noetheorovské okruhy; fundamentálna veta aritmetiky, Gaussovské okruhy.Okruhy polynómov (Aluffi, kapitola 7)
polynómy, okruhy polynómov; delenie polynómov so zvyškom; konečné okruhy; konečné vektorové priestory; rozklad polynómu na ireducibilné činitele; fundamentálna veta algebry; ireducibilné polynómy v![$\mathbf{R}[x]$ $\mathbf{R}[x]$](/KMAT/LinAlgeLinearneProgramovanie?action=AttachFile&do=get&target=latex_2b3a3d6166853353821e469d1a3ef79932522ba9_p1.png) ; ireducibilita v
; ireducibilita v ![$\mathbf{Q}[x]$ $\mathbf{Q}[x]$](/KMAT/LinAlgeLinearneProgramovanie?action=AttachFile&do=get&target=latex_1e00f059b7edbd3719e6b0b6e0fdcaceb3703984_p1.png) a
a ![$\mathbf{Z}[x]$ $\mathbf{Z}[x]$](/KMAT/LinAlgeLinearneProgramovanie?action=AttachFile&do=get&target=latex_24783f2de6052870ce65b65b9d2be8a9dec78ced_p1.png) , Gaussova lema;
, Gaussova lema; ![$\mathbf{Z}[x]$ $\mathbf{Z}[x]$](/KMAT/LinAlgeLinearneProgramovanie?action=AttachFile&do=get&target=latex_24783f2de6052870ce65b65b9d2be8a9dec78ced_p1.png) je PID, rozklad polynómu na ireducibilné činitele v
je PID, rozklad polynómu na ireducibilné činitele v ![$\mathbf{Z}[x]$ $\mathbf{Z}[x]$](/KMAT/LinAlgeLinearneProgramovanie?action=AttachFile&do=get&target=latex_24783f2de6052870ce65b65b9d2be8a9dec78ced_p1.png) , Gaussov test ireducibility v
, Gaussov test ireducibility v ![$\mathbf{Q}[x]$ $\mathbf{Q}[x]$](/KMAT/LinAlgeLinearneProgramovanie?action=AttachFile&do=get&target=latex_1e00f059b7edbd3719e6b0b6e0fdcaceb3703984_p1.png) .
. Lineárne zobrazenie
Vlastné číslo matice, vlastný vektor matice, charakteristický polynóm matice, ortogonálna podobnosť matíc
Polynómy s maticovými premennými
Jordanov kanonický tvar matice
Geometria a transformácie n-rozmerného euklidovského priestoru
Bilineárne a kvadratické formy a ich aplikácie, metóda najmenších štvorcov
Doporučená a použitá literatúra
- P. Aluffi, Algebra: Notes from underground, Cambridge University Press, Cambridge, UK, 2021.
T. Katriňák, M. Gavalec, E. Gedeonová, J. Smítal: Algebra a teoretická aritmetika 1, Alfa, Bratislava, 1985 & Univerzita Komenského, Bratislava, 1995 & Univerzita Komenského, Bratislava, 1999.
- J. J. Rotman, A first course in abstract algebra, 3rd. ed., Prentice Hall, NY, 2005.
- P. Zlatoš: Lineárna algebra a geometria, Albert Marenčin PT, Bratislava, 2011.
http://thales.doa.fmph.uniba.sk/zlatos/la/zlatos_LAG.pdf (kniha)
http://thales.doa.fmph.uniba.sk/zlatos/la/LAG_A4.pdf (A4)
- J. Gallian, Contemporary abstract algebra, 9th ed.,Centgage Learning, Boston, MA,2013.
- J. Guričan: Vybrané kapitoly z algebry.
http://thales.doa.fmph.uniba.sk/gurican/vka/vka2014_09_24.pdf
- Š. Schwarz: Základy náuky o riešení rovníc, SAV, Bratislava, 1968.
- J. Galanová, J. Gatial, P., Kaprálik: Lineárna algebra, STU, Bratislava, 2002.
- M. Zajac: Príklady Lineárna algebra 2.
prikladyLA2.ps, prikladyLA2.pdf (7.4.2021)
- M. Zajac: Zbierka úloh Lineárna algebra 2.
zbierkauloh.ps, zbierkauloh.pdf
jordanovtvar.ps, jordanovtvar.pdf
- M. Zajac: Prednášky Lineárna algebra 2.
prednaska1.ps, prednaska1.pdf (27.4.2020)
prednaska1a.ps, prednaska1a.pdf (13.3.2020)
https://xpopikt-didactic-application.herokuapp.com/
predn2.ps, predn2.pdf (27.4.2020)
predn3.ps, predn3.pdf (5.6.2020)
Hodnotenie
Časti hodnotenia
- Priebežné hodnotenie
Písomka 1 (???, 45 minút)
Písomka 2 (???, 45 minút)
Náhradná písomka (???)
- Skúška:
- Príklady (120 minút)
Obsah
- Priebežné hodnotenie:
- Písomka 1: 2 príklady z okruhov 1 - 6
- Písomka 2: 2 príklady z okruhov 7 - 12
- Skúška:
- 3 príklady z okruhov 1 - 6
- 3 príklady z okruhov 7 - 12
Bodovanie
- Priebežné hodnotenie:
Písomka 1 - 2: Za každý príklad sa dá získať 5 bodov
- Skúška:
Príklady: za 6 príkladov možno získať najviac 80 bodov, hodnota každého príkladu je vyznačená v zadaní skúšky
Pravidlá bodovania
- Priebežné hodnotenie:
súčasťou správneho riešenia je správny a kompletný postup, ak sú v riešení chyby, body sa udeľujú za časti, ktoré nie sú chybami ovplyvnené. Pri použití postupu, ktorý sa nepreberá v rámci predmetu, ho treba v riešení dostatočne exaktne zdôvodniť, inak za takýto postup nemusia byť udelené body. Za zdôvodnenie sa považuje napríklad referencia na všeobecne známe platné tvrdenia a dôkaz, že tento postup z nich vyplýva.
- Skúška:
Príklady: 'súčasťou správneho riešenia je správny a kompletný postup, ak sú v riešení chyby, body sa udeľujú za časti, ktoré nie sú chybami ovplyvnené. Pri použití postupu, ktorý sa nepreberá v rámci predmetu, ho treba v riešení dostatočne exaktne zdôvodniť, inak za takýto postup nemusia byť udelené body. Za zdôvodnenie sa považuje napríklad referencia na všeobecne známe platné tvrdenia a dôkaz, že tento postup z nich vyplýva.
Úspešnosť požadovaná na absolvovanie predmetu:
- Priebežné hodnotenie:
súčet bodových hodnotení písomiek aspoň 40%
- Skúška:
pri úspešnom splnení predpokladov skúšky sa získané body zarátavajú do hodnotenia skúšky
priebežné hodnotenie + príklady, aspoň 56 %
Váha pri výpočte známky
- Priebežné hodnotenie: 20 % (minimálne 8b, maximálne 20b)
- Skúška: 80 % (minimálne 36b, maximálne 80b)
Známka - body z intervalu [0;100+bonus]:
- Fx: body v intervale [ 0;56)
- E : body v intervale [56;65)
- D : body v intervale [65;74)
- C : body v intervale [74;83)
- B : body v intervale [83;92)
- A : body v intervale [92;inf)
Neúčasť/neúspešnosť na priebežnom hodnotení
Náhradnú písomku môže študent/ka absolvovať v prípade, ak mal/a ospravedlnenú neúčasť na jednej z priebežných písomiek. Náhradná písomka sa bude písať pred riadnym termínom skúšky.
Ospravedlnená neúčasť na oboch priebežných písomkách bude riešená individuálne s prednášajúcim a cvičiacim.
Neúčasť/neúspešnosť na skúške
Pri skúške je nárokovateľný opravný termín, teda na absolvovanie skúšky sú k dispozícii 2 termíny, spravidla, ale nie nutne, sú to Riadny termín a Opravný termín
- Pri neúčasti na Riadnom termíne alebo Opravnom termíne je možné si tento termín nahradiť na Náhradnom termíne
- Ospravedlnená neúčasť na 2 alebo viacerých termínoch z Riadneho termínu, Opravného termínu a Náhradného termínu bude konzultovaná individuálne s prednášajucim(i).
Priebeh priebežného hodnotenia a skúšky
Ak niekto potrebuje pri Priebežnom hodnotení a Skúške špeciálne podmienky, napríklad zo zdravotných dôvodov, prosím, napíšte mi e-mail na jan.karabas@stuba.sk .
Na stole na viditeľnom mieste treba mať:
- študentský preukaz
Okrem toho môže byť na stole iba (nedodržanie má za následok hodnotenie Fx):
- perá
- nápoje
- zo zdravotných dôvodov aj potraviny, lieky...
zošité oficiálne, nie vlastné papiere k písomke/skúške
Smie sa používať:
- perá, také množstvo, aby sa nevypísali
zošité oficiálne, nie vlastné papiere k písomke/skúške
Nesmie používať a nesmie byť v dosahu (nedodržanie má za následok hodnotenie Fx):
- všetko ostatné, špeciálne mobily, tablety, počítače, Bluetooth slúchadlá a ďalšie komunikačné zariadenia
Ďalšie pokyny:
- treba písať v pridelenej miestnosti na pridelenom mieste podľa rozpisu
riešenie príkladu/otázky X treba vypracovať na oficiálny papier so zadaním príkladu/otázky X (časti riešenie príkladu/otázky X nenachádzajúce sa na na oficiálnom papieri so zadaním príkladu/otázky X sa neberú do úvahy pri bodovaní riešenia/odpovede príkladu/na otázku X)
- počas skúšky nie je možné odísť z miestnosti, teda pred odchodom treba odovzdať finálnu verziu riešení
Pozor
Základným zdrojom pre Lineárnu algebru 2 sú prednášky, cvičenia a odporúčaná literatúra. Videá, texty a online materiály sú iba doplnkový zdroj, nie je garantované, že obsahujú všetko a vo vhodnej forme, čo bude požadované pri priebežnom hodnotení a na skúške.
Staršia verzia prednášky
Pole
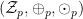
prednáška text: prednaska1.pdf, strany 1, 5 - 7, 13
prednáška video: https://youtu.be/RYShvddtXx0 a https://youtu.be/UuxRy0ySiI8
cvičenie text: prikladyLA2.pdf, týždeň 2, príklady 1 - 5, 7 - 8, týždeň 3, príklad 6, časti b - d, týždeň 4, príklady 1 - 2, 5
cvičenie video: https://youtu.be/WTn10sOhL88 a https://youtu.be/E1u89_4PAz4
rozdiely: tabuľka pre rozšírený Euklidov algoritmus má 4 stĺpce, pri riadkovo ekvivalentných úpravách sa nemôže vynechávať ani nulový riadok, pri riešení sústavy lineárnych rovníc sa matica upravuje do redukovaného stupňovitého tvaru, riešenie sústavy lineárnych rovníc sa zapisuje do stĺpca
Pole
![$(\mathcal{Z}_p[x],\oplus_p,\odot_p)/_{(p(x))}$ $(\mathcal{Z}_p[x],\oplus_p,\odot_p)/_{(p(x))}$](/KMAT/LinAlgeLinearneProgramovanie?action=AttachFile&do=get&target=latex_2e78e7aeff067b4e6367357a80815edc2fd3deb7_p1.png)
prednáška text: prednaska1.pdf, strany 8 - 10
prednáška video: https://youtu.be/z94noc6YFAk a https://youtu.be/Hz4GsqVIaao a https://youtu.be/UuxRy0ySiI8
cvičenie text: prikladyLA2.pdf, týždeň 2, príklady 6, časť b, 9 - 10, týždeň 3, príklady 1 - 5
cvičenie video: https://youtu.be/bwksRJg8mCc a https://youtu.be/RGep5pY-72M a https://youtu.be/E1u89_4PAz4
rozdiely: množina všetkých polynómov nad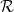 v neurčitej
v neurčitej  je označená
je označená ![$\mathcal{R}[x]$ $\mathcal{R}[x]$](/KMAT/LinAlgeLinearneProgramovanie?action=AttachFile&do=get&target=latex_aa1b2d99015de8e1bb5c8d26e08231d02257978d_p1.png) , tabuľka pre rozšírený Euklidov algoritmus má 4 stĺpce
, tabuľka pre rozšírený Euklidov algoritmus má 4 stĺpce
Pole
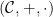
prednáška text: prednaska1.pdf, strany 1 - 5
prednáška video: https://youtu.be/Ja7oYlKlIwU a https://youtu.be/8kZk1FA82gE a https://youtu.be/saXHS6yLwms
cvicenie text: priklady1.pdf, kapitola 5
cvicenie video: N/A
rozdiely:
Sústava lineárnych rovníc nad okruhom
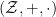
prednáška text: prednaska1a.pdf
prednáška video: https://youtu.be/UuxRy0ySiI8 a https://youtu.be/zlVjszq8HRA
cvičenie text: prikladyLA2.pdf, týždeň 4, príklad 3
cvičenie video: https://youtu.be/tIivbL7qnJk
rozdiely: pri riadkovo ekvivalentných úpravách sa nemôže vynechávať ani nulový riadok, riešenie sústavy lineárnych rovníc sa zapisuje do stĺpca, Hermitov tvar matice nemusí spĺňať hodnosť matice = počet riadkov < počet stĺpcov, pred-Smithov tvar matice, Smithov kanonický tvar matice
Lineárne zobrazenie
prednáška text: prednaska1.pdf, strany 21 - 24
prednáška video: https://youtu.be/GQ3zfpvBz0Q
cvičenie text: prikladyLA2.pdf, týždeň 6, príklady 1, 3, týždeň 7, príklady 1 - 2
cvičenie video: https://youtu.be/KcCSe5xBCrg
rozdiely: lineárne zobrazenie sa nazýva lineárne zobrazenie, obraz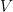 v lineárnom zobrazení
v lineárnom zobrazení 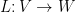 sa označuje
sa označuje 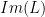 , vektor sa zapisuje do stĺpca, matica lineárneho zobrazenia
, vektor sa zapisuje do stĺpca, matica lineárneho zobrazenia 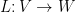 s bázou
s bázou 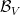 vo
vo 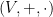 a bázou
a bázou 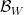 vo
vo 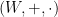 sa označuje
sa označuje 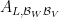
Podobnosť matíc, vlastné číslo matice, vlastný vektor matice, charakteristický polynóm matice
prednáška text: predn2.pdf, strany 4, 6 - 7
prednáška video: https://youtu.be/UvOFYLZBv0k a https://youtu.be/VPr_b_6Ijzc
cvičenie text: prikladyLA2.pdf, týždeň 7, príklady 1, 3, týždeň 8, príklady 1 - 2
cvičenie video: https://youtu.be/upuCd9MzF48 a https://youtu.be/aHUYI63EmKw
rozdiely: vektor sa zapisuje do stĺpca, charakteristický polynóm matice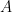 môže byť aj
môže byť aj 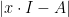 , pri riadkovo ekvivalentných úpravách sa nemôže vynechávať ani nulový riadok
, pri riadkovo ekvivalentných úpravách sa nemôže vynechávať ani nulový riadok
Jordanov kanonický tvar matice
prednáška text: predn2.pdf, strany 7 - 10
prednáška video: https://youtu.be/VPr_b_6Ijzc a https://youtu.be/Y0iPM9DxAGI
cvičenie text: prikladyLA2.pdf, týždeň 8, príklad 4, týždeň 9, príklad 1
cvičenie video: https://youtu.be/aHUYI63EmKw a https://youtu.be/HjO8QYFyDcM
rozdiely: Jordanov blok má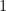 nad diagonálou, do matice prechodu od novej bázy zo zovšeobecnených vlastných vektorov k starej báze sa reťazec zovšeobecnených vlastných vektorov
nad diagonálou, do matice prechodu od novej bázy zo zovšeobecnených vlastných vektorov k starej báze sa reťazec zovšeobecnených vlastných vektorov 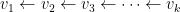 zapisuje zľava od vlasného vektoru aka
zapisuje zľava od vlasného vektoru aka 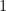 -zovšeobecneného vlastného vektoru
-zovšeobecneného vlastného vektoru 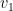 doprava po
doprava po 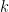 -zovšeobecnený vlasný vektor
-zovšeobecnený vlasný vektor 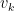
Minimálny polynóm matice, minimálny polynóm vektoru vzhľadom na maticu, matica pridružená k polynómu
prednáška text: predn2.pdf, strany 1 - 3
prednáška video: https://youtu.be/UvOFYLZBv0k a https://youtu.be/Y0iPM9DxAGI a https://youtu.be/VPr_b_6Ijzc
cvičenie text: prikladyLA2.pdf, týždeň 7, príklady 5 - 8, týždeň 8, príklad 3
cvičenie video: https://youtu.be/upuCd9MzF48 a https://youtu.be/aHUYI63EmKw
rozdiely: matica pridružená k polynómu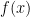 stupňa
stupňa 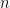 má
má 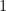 nad diagonálou a koeficienty normovaného polynómu asociovaného s
nad diagonálou a koeficienty normovaného polynómu asociovaného s 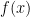 okrem vedúceho v stĺpci
okrem vedúceho v stĺpci 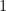 pričom v riadku
pričom v riadku 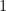 je koeficient pri
je koeficient pri 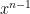 a v riadku
a v riadku 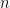 je koeficient pri
je koeficient pri 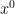
Metóda najmenších štvorcov, ortonormálna matica, ortonormálna podobnosť matíc
prednáška text: predn3.pdf, strany 1 - 5
prednáška video: https://youtu.be/mrI6qAWy0iI
cvičenie text: prikladyLA2.pdf, týždeň 10, príklady 1 - 4, týždeň 11 - 12, príklad 1
cvičenie video: https://youtu.be/yN9iUoRFIeM
rozdiely: vektor sa zapisuje do stĺpca, neznáme koeficienty aproximačného polynómu zodpovedajú stĺpcom matice príslušnej sútavy lineárncyh rovníc v poradí zľava doprava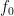 ,
, 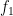 ,
, 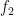 , ...,
, ..., 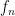
Zhodné zobrazenie v
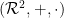 , zhodné zobrazenie v
, zhodné zobrazenie v 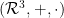
prednáška text:
prednáška video: https://youtu.be/rfHMNLuqudM
cvičenie text: prikladyLA2.pdf, týždeň 11 - 12, príklady 2 - 4
cvičenie video: https://youtu.be/gzbHSHVUU-E
rozdiely: vektor sa zapisuje do stĺpca
 Oddelenie matematiky
Oddelenie matematiky